こんにちは芸術家の弘也です。
芸術品を鑑賞しているといたる所に黄金比が使われていることが分かります。それは、黄金比と知って計算された作品もあれば、美しい物を作ったら自然になっていた作品もあることでしょう。
自分が制作する上でも、芸術鑑賞を楽しむ上でも知っておいて損はないので、紹介します。
・デザイン学習者
・芸術鑑賞が好きな方
黄金比とは
数式で次のように表すことができます。
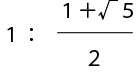
これでは分かりにくいですね。これから簡単に表していきますので、ご安心ください。
まず、黄金比というくらいですから、比率の話になります。
近い数字では1:1.618… と表すことができます。右側は割り切れないため…となっています。円周率などと同じ無理数ということですね。
もっと分かりやすい数字でいえば、「3:5」「5:8」「8:13」などと表すことができます。こちらの方が覚えやすく使いやすいですね。ただしこれらは、整数で表せる近い比率ですので、正確ではないことに注意してください。
なぜ美しいとされているのか
人の感覚によって美しいとされ、世界各国で古くから親しまれてきています。しかし、科学的な根拠はないとされているようです。また、無理数のため正確な黄金比は現実には存在しないとして、都市伝説だとする意見もあります。
しかし、美しいとする人が多い以上神秘的な魅力をもった比率といえるでしょう。
黄金長方形
辺の長さが1:1.618となっている長方形を黄金長方形と呼びます。
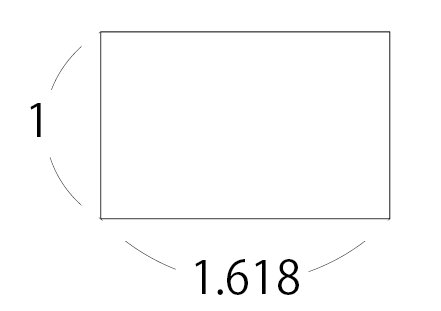
名刺やクレジットカード、タバコのケースなど、あらゆる場面に近似値が使われていると言われてます。
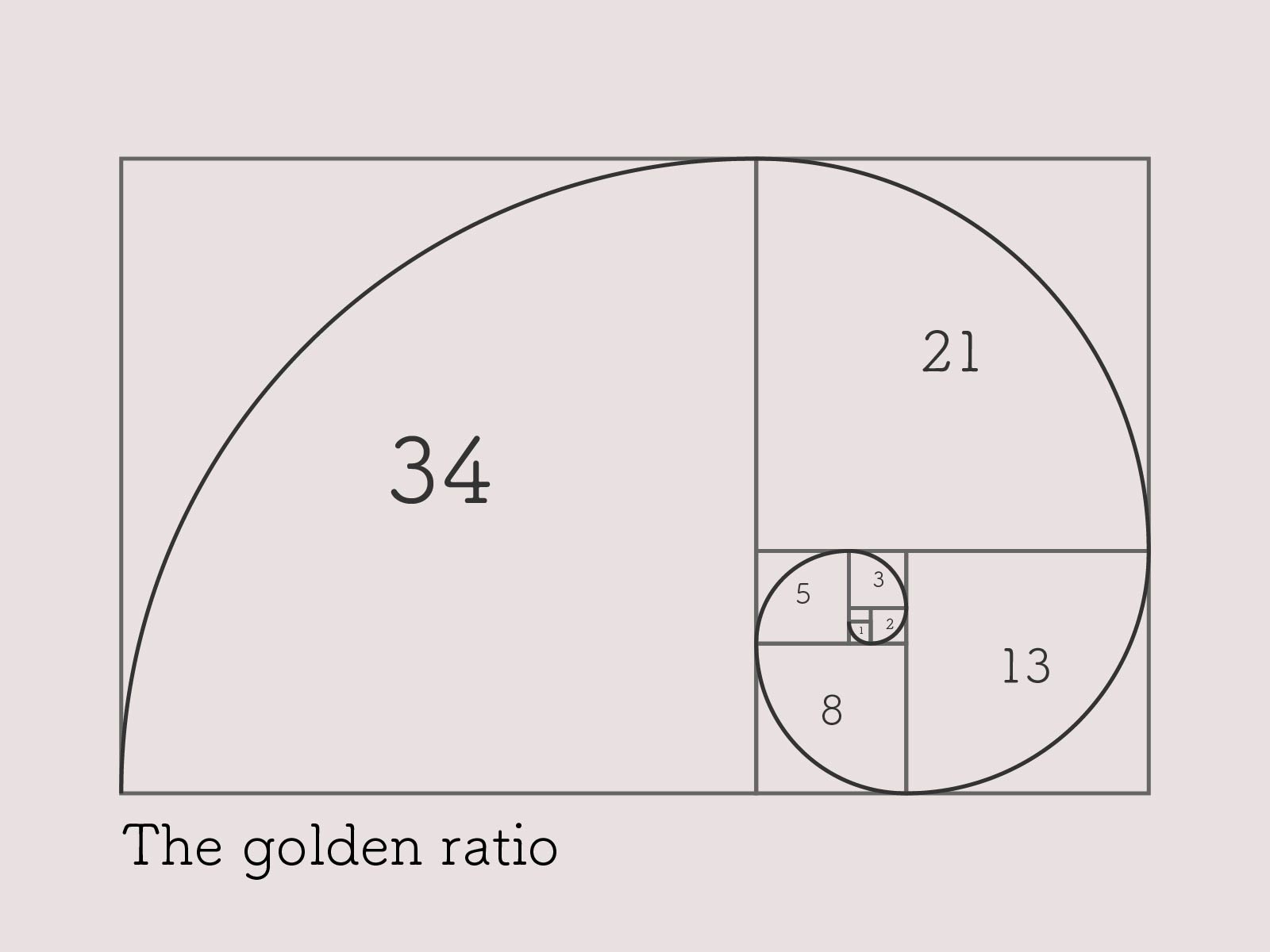
黄金螺旋
黄金長方形を並べ、対角線をなめらかに繋いでいくと、渦巻き状の螺旋を描くことができます。これが「黄金螺旋」です。
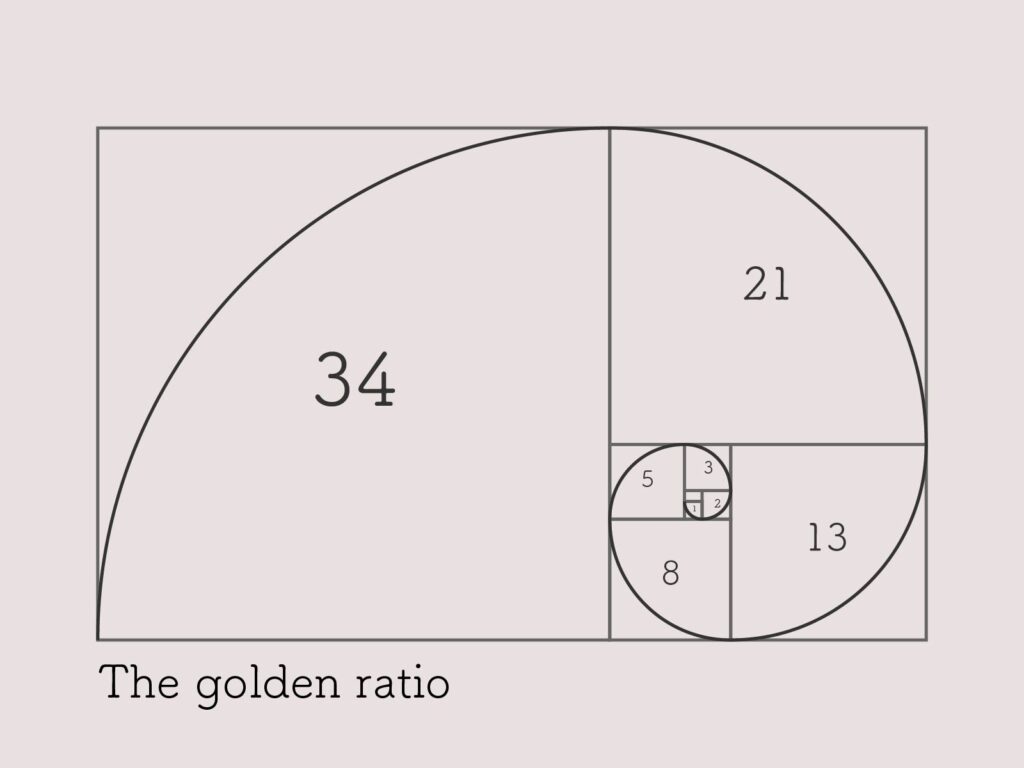
この黄金螺旋は自然界でもよく使われています。
・オウム貝の殻
・ひまわりの種
・松ぼっくり
などに見られます。
芸術作品
やはり美しいと言われるだけに、芸術作品には数多く使われています。
- モナリザ
顔の輪郭が1:1.618になっています。
- ミロのビーナス
頭〜へそが1 : へそ〜足が1.618になっています。
他にも、
- 冨嶽三十六景
- パリの凱旋門
などは使われているとよく取り上げられています。
企業ロゴ
企業のロゴに取り入ることも多いですね。
- Apple
これらのロゴは細部に至るで黄金比が確認されています。
フィボナッチ数列と黄金比
フィボナッチ数列とはその1つ前の数と2つ前の数の和になる数列のことです。
1、1、2、3、5、8、13、21、34、55、89、148….
このような数列になります。そして、隣合う数字の比率を見てください。
最初は1:1ですが、1:2、2:3となっていきます。
そして89:148の比を簡単にすると1:1.662…となります。そうです、黄金比に近づいていきます。
最終的に、フィボナッチ数列の隣り合う数の比率は黄金比に収束します。
このことからもフィボナッチ数列は黄金比と密接に関わっており、美しい数列とも言われています。
また、ひまわり、松ぼっくり、パイナップルなどにもフィボナッチ数列が使われていると言われています。
まとめ
1:1.618が黄金比であると学びました。この比率が形を変えて自然界から芸術品にまで活用されています。
これらは「黄金比をもとに作られた」ものもあれば、「美しいものを求めた結果、黄金比に近づいた」ものもあると思います。作品のデザインによって美しく視える比率が変わってくるでしょう。世の中全てが黄金比なんだ!と固くならず、複数ある比率のうちの一つという柔軟さも大切ではないでしょうか。



コメント